Расширив круг своих обязанностей, вы не только сможете доказать свою компетентность как лидера, но также продемонстрируете свою ценность как надежного сотрудника. Если вам удастся предложить своему начальству пути решения возникших кризисных ситуаций, это, безусловно, повысит вашу ценность в его глазах.
Сложение и вычитание отрицательных и положительных чисел — правило, формулы и примеры
Отрицательные числа начинают изучаться на уроках математики, как правило, с 6 класса, хотя иногда их обсуждение может начаться и раньше. Число с знаком «+» обозначает положительное число, тогда как число с противоположным знаком — это отрицательное.
Для того чтобы понять, как складываются и вычитаются положительные и отрицательные числа, очень удобно использовать координатную линию. На примере: давайте сложим числа -18 и 2. Нанесите на координатную линию число -18; далее, добавьте 2 единичные дроби, двигаясь вправо по линии. Таким образом, координатная линия покажет, что сумма равна -16.
Правило сложения отрицательных чисел и чисел с разными знаками
Чтобы произвести сложение двух отрицательных чисел, необходимо следовать определенному алгоритму:
- Сложите положительные значения (модули) двух чисел.
- К полученной сумме добавьте знак минус.
Рассмотрим пример: сумма чисел -9 и -6. В данном случае мы складываем их абсолютные значения 9 и 6, что в итоге дает натуральное число 15, и присваиваем ему знак «-«. Таким образом, мы получаем -15.
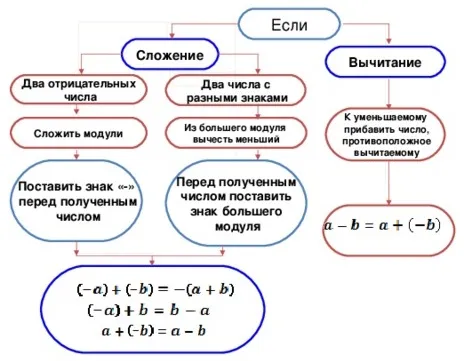
При складывании рациональных (дробных) чисел тот же алгоритм применим:
-26,35 + (-25,35) = -(26,35 + 25,35) = -51,75.
Мы просто прибавляем 25,35 к 26,35 (то есть складываем их модули) и получаем 51,75, после чего добавляем знак минус, так как оба числа были отрицательными.
Чтобы произвести сложение натуральных чисел с учетом знаков, используйте символы «+» и «-«: необходимо вычесть из большого числа сумму меньшего, а перед итогом поставить знак большего по модулю числа.
Например: 61,2 + (-31,5) = +(61,2 — 31,5) = 30,5.
Здесь модуль большего числа 61,2 является положительным, следовательно, результат положителен.
В случае, когда -81 + 35 = -(81 — 35) = -46, поскольку большее число имеет отрицательный знак, мы заменяем плюс на минус и получаем отрицательный ответ.
Как вычитать отрицательные и положительные числа
Для нахождения разности между противоположными числами, нужно прибавить к вычитаемому вычитаемое с противоположным знаком. Иначе говоря, замените знак вычитания суммой.
Этот процесс можно выразить следующей формулой:
Каждое математическое выражение с участием операций сложения и вычитания необходимо рассматривать как сумму чисел.
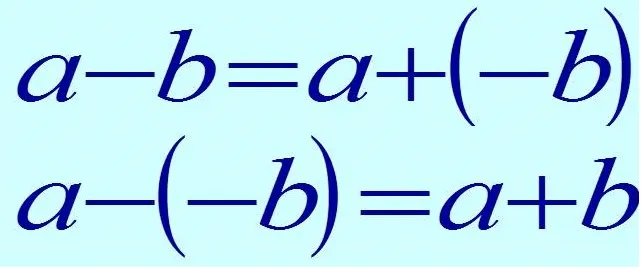
Рассмотрим пример:
-20 — 14 = -20 + (-14) = -34;
-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.
Разность выражения будет положительна, если уменьшающее число больше, чем вычитаемое; и отрицательна, если меньше. Если же вычитаемое и уменьшающее равны, то разность будет равна нулю.
Пример: 15 — 6 = 15 + (-6) = 9 — вычитаемое больше уменьшающего, следовательно результат положительный.
Пример: -15 — 6 = -15 + (-6) = -21 — в этом случае вычитаемое меньше, а значит результат отрицательный.
Если нужно вычесть отрицательное число, то два знака минус преобразуются в знак плюс.
Например: 10 — (-5) = 10 + 5 = 15;
-10 — (-5) = -10 + 5 = -5.
Все вышеперечисленные арифметические операции можно легко выполнить и с помощью калькулятора. Для этого достаточно ввести сначала модуль числа, а затем нажать клавишу смены знака.
Например, чтобы ввести число -81,73, нажмите клавиши в следующем порядке: «8», «1», «,», «7», «3», затем «+/-«. Для выполнения расчетов с отрицательными числами действуйте так же, как и с положительными.
Для полной математической точности необходимо также подтвердить следующее: 0 x V = 0 для любого элемента. Это следует из того, что 0 x V = (0 + 0) x V = 0 x V + 0 x V. Это означает, что добавление нуля к произведению n не меняет сумму множества. В конечном итоге, произведение равно нулю.
Отрицательные числа
Отрицательные числа – это числа, лежащие слева от нуля на числовой прямой. Это определение достаточно простое для понимания, но его восприятие иногда вызывает сложности. В реальной жизни, на первый взгляд, нет ничего отрицательного – трудно представить, что у вас есть, например, -2 яблока или -3 карандаша. Исключение составляет ситуация с долгами или отсутствием чего-либо.
По сути, любое отрицательное число может быть интерпретировано как отсутствие некоторых единиц. Например, -3 можно интерпретировать так: вы не добрали до нуля три единицы. Подобные негативные значения часто возникают в бухгалтерской отчетности и финансовых документах.
Правило знаков
Правило знаков, часто обсуждаемое на уроках математики в шестом классе, заслуживает особого внимания. Это связано с тем, что правило знака является результатом правил умножения для отрицательных и положительных чисел.
Так например:
6 — (-6) = 6 + (-1 * -1 * 6) = 6 + 6. Однако это очень длинный процесс, чтобы повторять его каждый раз. Проще запомнить заданное правило: умножение минуса на минус и плюса на плюс дает знак плюс. А если вы умножаете «плюс» на «минус», то результат будет «минус». Эти правила легко запоминаются, и вам не придется каждый раз вспоминать множественные правила.
Сложение и вычитание отрицательных чисел
Лучше рассмотреть каждый из процессов отдельно, чтобы избежать недоразумений.
Сложение отрицательных чисел
Сложение может выполняться между:
- Двумя отрицательными числами. В таком случае правило «минус» умноженный на «минус» дает «плюс». В результате мы получаем выражение, рассматриваемое в предыдущем пункте, и проводим сложение отрицательного числа с положительным. Здесь может потребоваться поменять местами числа и выполнить вычитание.
- С отрицательным и положительным числом. Это создает ситуацию, аналогичную сложению двух отрицательных чисел. Умножение «минуса» на «плюс» дает «минус». Полученные числа складываются по модулям, а затем «минус» добавляется к результату.
- Смешанную пару — положительные и отрицательные числа. Этот случай часто используется в примерах, поскольку преобразование «минус» в «минус» дает результат в форме «плюса». Следовательно, итогом будет сложение двух положительных чисел.
Обратите внимание, что прибавление или вычитание нуля не влияет на значение отрицательного числа. Однако, когда вы вычитаете из нуля, знак меняется на противоположный.
Для полной математической точности необходимо еще подтвердить, что 0 x V = 0 для каждого элемента. Логически, 0 x V = (0 + 0) x V = 0 x V + 0 x V. Это означает, что добавление коэфициента 0 x V никоим образом не изменяет сумму множества. В конечном итоге, произведение всегда равно нулю.
Математика для блондинок
Математика должна быть доступной для всех – и блондинки не являются исключением, они тоже должны уметь решать математические задачи.
Минус на плюс что дает?
Положительные и отрицательные числа были изобретены математиками, которые в какой-то момент решили, что им необходимо создать целую новую категорию для более точного описания чисел. Они разработали различные правила для умножения и деления положительных и отрицательных чисел, чтобы обеспечить удобство и четкость в расчетах и оформлениях. Нам нужно просто усвоить эти правила и применять их, как если бы мы отвечали математикам, что именно они ожидают от нас услышать.
Запомнить правила умножения и деления достаточно просто. Если два числа имеют разные знаки, результатом всегда будет отрицательное число. Если же два числа обладают одинаковым знаком, результат будет положительным.
Давайте рассмотрим все возможные комбинации. При умножении минуса на плюс мы получаем минус. Что же происходит, если мы умножаем и делим два отрицательных числа? При этом мы получаем результат со знаком плюс.
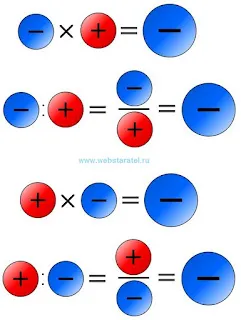 |
| Минус на плюс, плюс на минус. |
Таким образом, все возможные операции умножения и деления положительных и отрицательных чисел покрыты. Однако понятие знака плюс остается до сих пор не объясненным. Это правило мы создали для себя, чтобы удобно запомнить его. Что утверждают математики в этом отношении? При умножении или делении положительных и отрицательных чисел всегда получается отрицательное число, вне зависимости от порядка.
Что дает минус на минус? Умножая или деля два отрицательных числа, вы всегда получаете положительное число. Каков результат множительного действия двух положительных чисел? Умножение или деление плюса на плюс всегда дает результат, имеющий знак плюс.
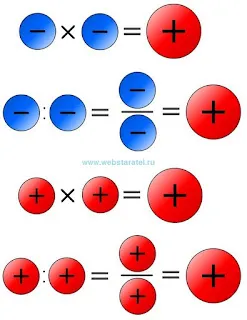 |
| Минус на минус, плюс на плюс. |
Надеюсь, вам стало понятно: минус на минус дает плюс, а плюс на плюс также дает плюс. Что скажут математики? Умножая или деля положительные или отрицательные числа, вы всегда получаете положительное число.
Если запомнить, что умножение и деление положительных чисел всегда дает то же положительное число, то можно столкнуться с трудностью в случае, когда речь идет об умножении и делении двух отрицательных чисел. На интуитивном уровне ожидается, что два отрицательных числа должны давать отрицательный результат, однако это не так. Как же два знака минус превращаются в знак плюс?
Математики, действительно, интуитивно решили задачу правильного определения способа умножения и деления плюсов и минусов. Правила были записаны в учебниках без излишних подробностей, что упрощает их понимание. Чтобы четко ответить на данный вопрос, важно осознать, что обозначают знаки плюс и минус в математическом контексте.
У всего есть две стороны – положительная и отрицательная. Научитесь воспринимать это не только на примере объективных предметов, таких как аккумулятор, но и рассматривать на примере человеческого характера. Каждая черта характера имеет свои положительные и отрицательные аспекты.
Примеры умножения отрицательных чисел
Пример 1. Выполните вычисления: (-2)∗(-2) и (-3)∗(-7).
Не забывайте правило: когда вы умножаете отрицательное число на другое отрицательное число, результат будет положительным. Рассчитаем:
Пример 2. Узнайте сумму: (-11)∗11 и (-20)∗2.
Помните, что умножение отрицательного числа на положительное число даст результат со знаком минус. Рассмотрим подробнее:
Пример 3. Вычислите произведения 5∗(-5) и 12∗(-8).
Не забывайте правило: произведение положительного числа на отрицательное число всегда даст отрицательный результат. Давайте выполнем соответствующие вычисления: