Два угла являются перпендикулярными, если их стороны представляют собой дополнительные лучи, которые образуют 90-градусный угол. Существенным свойством прямых углов является то, что все они равны друг другу, независимо от расположения или контекста.
Как получить «пятерку» по геометрии
Данная статья написана и проверена на точность и полноту нашей квалифицированной командой редакторов и исследователей, что обеспечивает ее высокое качество информации.
Команда управления контентом wikiHow осуществляет тщательный контроль над работой редакторов для гарантии того, что каждая статья соответствует установленным нами высоким стандартам качества.
В статье использовано 14 источников, которые заинтересованные читатели могут найти в конце текста.
Количество просмотров данной статьи составляет 39 804, что свидетельствует о ее актуальности и популярности.
Геометрия, как научная дисциплина, изучающая формы и углы, иногда может показаться сложной для многих учащихся. При первом контакте с геометрией большинство концепций выглядят совершенно новыми и могут вызывать путаницу. Данная область знаний включает множество аксиом, теорем, определений и символов, которые необходимо освоить, чтобы в дальнейшем сформировать полное понятие. К счастью, проявление хороших учебных привычек и следование нескольким практическим рекомендациям смогут значительно облегчить процесс изучения геометрии.
Как получать высокие оценки

- Не бойтесь задавать вопросы на уроках. Учитель в классе как раз для того, чтобы помочь разобраться в сложных темах. Если возникает вопрос, смело обращайтесь к нему, ведь, вероятно, другие учащиеся также интересуются тем же вопросом.
- Подготовьтесь к урокам, заранее изучая соответствующие разделы учебника. Это включает в себя разбор формул, теорем и аксиом, чтобы вы могли легко следовать за учителем.
- Во время лекций активно слушайте учителя. У вас всегда будет возможность обсудить материал с одноклассниками во время перерыва или после уроков.
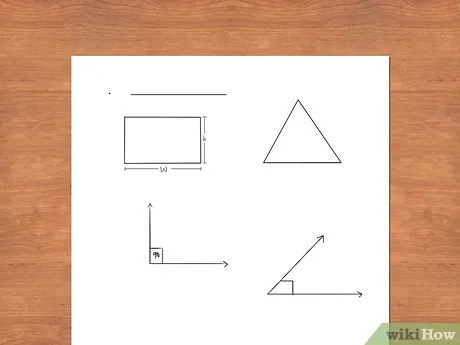
- Представляйте фигуры, изучаемые в геометрии, на схемах и рисунках. Это поможет вам лучше понять свойства различных фигур и облегчить их изучение.
- Старайтесь распознавать геометрические фигуры, находя их в различных ориентациях на основе их свойств: величины углов, наличия параллельных и перпендикулярных линий и т.д.

- Скорее всего, среди ваших одноклассников есть такие, кто прекрасно понимает материал. Обратитесь за помощью к ним, и кроме того, объясняя материал своим друзьям, вы сами лучше его усвоите.

- При измерении углов с помощью транспортира следует:
- уместить центральное отверстие транспортира на острие угла;
- повернуть транспортир так, чтобы его прямая основание совпало с одной из сторон угла;
- продлить вторую сторону угла до арки транспортира и записать величину угла, где они пересекаются. Это и есть измеряемый угол.

- Во время выполнения домашней работы вы получите возможность неспешно повторить пройденный материал и уделить особое внимание сложным моментам для их лучшего понимания. Не стесняйтесь обращаться за помощью к учителям или одноклассникам в случае возникновения вопросов.

- Попробуйте обучить геометрии своего брата, сестру или родителей. Объясняйте интересные темы в учебной группе, где вы уверены в своих знаниях.

Когда начинают изучать геометрию в школе? Зачем она нужна?
В процессе школьного обучения до 7 класса учащиеся изучают общую математику, а в 7 классе преподавание делится на две отдельные дисциплины: алгебру и геометрию.
Для многих школьников геометрия ассоциируется с непонятными формулами и расчетами, которые, на их взгляд, не находят практического применения в жизни. Однако цель изучения этой дисциплины далеко не в том, чтобы усложнять жизнь учащимся и ухудшать их оценки.
Безусловно, курс геометрии представляет огромную ценность для таких профессий, как архитектура, строительство и дизайн, а также может пригодиться при выполнении различных домашних задач, например, при ремонте квартиры или оформлении интерьера. Однако, задаваясь вопросом, о необходимости изучения геометрии, стоит отметить, что знание данной дисциплины является фундаментальным навыком, развивающим логическое и критическое мышление, что несомненно пригодится в жизни.
Несмотря на то что 99% теорем и формул, которые вы изучаете, могут не понадобиться вам в повседневной жизни, решение задач и понимание геометрических концепций положительно сказываются на развитии вашего умственного потенциала и гибкости мышления, что особо важно в нестандартных ситуациях.

Почему дети не понимают геометрию?
Причины
- Недостаток заинтересованности со стороны учителя или репетитора в качественном объяснении теоретических аспектов геометрии учащимся.
После летних каникул дети, приходя в 7 класс, часто хотят быть более свободными, гулять и общаться с друзьями. И тут они сталкиваются с необходимостью изучения новых, сложных понятий и решений задач, которые могут казаться абсурдными. Учителям важно пробудить у детей интерес к геометрии и показать, как она соотносится с реальной жизнью. Можно применять наглядные примеры, чтобы удержать внимание учащихся.
Рассматривая, как ученики обращаются к учителю с вопросами о смысле изучаемого материала, можно выявить, что часто диалог выглядит так:
— А зачем нам проходить геометрию каждый год? «Ну, это просто часть учебного плана», — параллельно отвечают учителя.
- Дети могут намеренно игнорировать изучение предмета.
Несмотря на то, что им может быть не совсем понятно, чего именно они должны изучать, это порождает отторжение и нехватку желания погрузиться в основы. Невозможность усваивать материал и отсутствие фундамента создают эффект снежного кома: без понимания основ сложно решать даже простейшие задачи.
Следует отметить, что не все учебники передают информацию логично и доступно. У некоторых из них информация кажется перегруженной и невыносимой, что делает обучение еще более сложным.
Как можно ожидать, что ученик сможет понять геометрию, если он боится задать вопрос в классе? Некоторым учителям следует учитывать, что осмеивание и унижение ученика перед классом сыграет не последнюю роль в формировании у его психики отвращения к предмету. Это особенно печально, но такие случаи, к сожалению, имеют место быть.
Настоящий учитель выступает в роли партнера для своих учеников. Взаимоотношения, которые складываются между педагогами и детьми, должны основываться на доверии и поддержке.
С чего начать изучение
Перед тем как приступить к изучению нового материала, осознайте, что ни один процесс обучения не происходит мгновенно. Необходимо время, и его количество вполне зависит от поставленной вами цели. Если ваша цель — лишь добиться хорошей оценки на контрольной, то достаточно изучить конкретную тему и выполнить несколько практических задач.
Просмотрите последние несколько абзацев учебника, не спешите, но постарайтесь усвоить основные идеи. После этого попробуйте решить несколько практических задач для закрепления знаний. Часто возвращайтесь к тексту вашего учебника и стремитесь выделить алгоритмы для успешного решения задач.
Если у вас возникнут трудности в начале обучения, не расстраивайтесь. Главное — это упорство и желание не останавливаться перед сложностями. Порой имеет смысл обратиться к опубликованным учебникам или справочникам, чтобы не просто копировать готовые решения, но и постараться понять логику, лежащую в их основе. Если ранее мы упоминали о схожей задаче на уроке, стоит вспомнить слова учителя; возможно, они окажутся полезными для вас в трудный момент.
Не забывайте о помощи со стороны ваших одноклассников. Иногда одноклассники, друзья или близкие могут гораздо быстрее разобраться в проблеме, чем взрослые.

Обратите внимание, когда перед вами стоит серьезная задача углубленного изучения предмета. В этом случае потребуются колоссальные усилия, и главным действительно станет ваша мотивация, что необходимо помнить. Самостоятельное решение задач заключается в многократном повторении, а не в простом копировании готовых решений из Интернета. Регулярность и системный подход в обучении также играют важную роль; очень полезно будет выделять полчаса или даже час в день исключительно на геометрию.
Только с помощью практики вы сможете не только достичь своей цели, но и осознанно освоить материал на должном уровне. Постарайтесь каждый день решать по одной-две задачи, что вскоре станет вашим обычаем. Со временем вам станет легче решать задачи, а найденные ответы будут приносить удовлетворение.
Если в классе рассматривается какая-то сложная проблема, и преподаватель предлагает вам попробовать решить ее на доске, не стесняйтесь отвечать, даже если у вас нет полной уверенности в своих действиях. Начните рассуждать, чтобы задействовать свое мышление. Преподаватели всегда рады видеть искренний интерес своих студентов. Ваши аргументы вполне могут стать основой для новой библиотеки знаний, к которой преподаватель будет рад добавить свою помощь. Уделите внимание правильному направлению ваших мыслей; в результате вы запомните алгоритмы решений и сможете использовать их при возникновении аналогичных задач в будущем.
Использовать по желанию
Если геометрия дается с большими сложностями или требуется понимание материала на более глубоком уровне, можно рассмотреть возможность занятий с репетитором. Уроки индивидуально, эквивалентные занятия с репетитором почти всегда показывают хорошие результаты. При этом нет необходимости встречаться со специалистом лично. Благодаря современным технологиям можно удобно организовать онлайн-занятия через Skype или другие подобные приложения.
Итак, это все советы, которые вам могут понадобиться. Ничего слишком сложного, а при этом полезность этих рекомендаций велика. Просто следуйте этим рекомендациям, и вы вскоре заметите значительные успехи в изучении геометрии.
Четырехугольники
На уроках геометрии много говорится о четырехугольниках, таких как прямоугольник, квадрат, ромб.
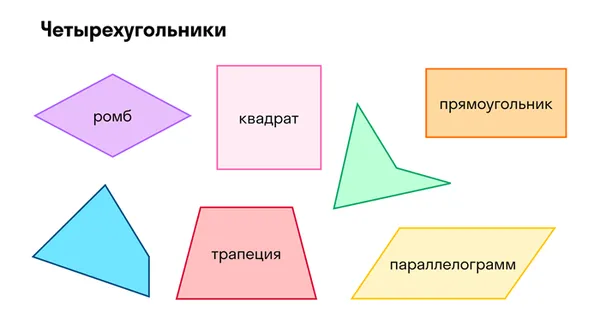
Однако мы не обсуждаем их так детально, как те же треугольники, например, теоремы о синусе и косинусе. Свойства, которые можно выразить, относятся лишь к определенным категориям четырехугольников.
Следует уделить внимание изучению четырехугольников, так как каждый из них обладает уникальными свойствами, которые могут не быть применимы к другим фигурам. Поэтому лучше всего тщательно изучить каждый вид четырехугольников на уроках или воспользоваться дополнительными материалами, чтобы понять:
- площадь фигуры;
- периметр фигуры;
- площадь прямоугольника;
- периметр прямоугольника;
- площадь квадрата;
- периметр квадрата;
- особенности параллелограмма;
- прямоугольный параллелепипед.
Практическая сторона геометрии
Название «геометрия» происходит от греческих слов: «geo», что означает земля, и «metreo», что означает мера. Изначально геометрия использовалась для разметки земель и конструирования различных сооружений. Тем не менее, ее применение гораздо более широко и разнообразно.
Чтобы действительно понять актуальность геометрии в повседневной жизни, достаточно оглянуться вокруг: геометрия окружает нас повсюду, от форм предметов до функциональности их дизайна. Например, круг в своем основании применим в искусстве, строительстве и ряде технических устройств. Аналогично, многие другие геометрические формы жизненно важны при проектировании автомобилей, смартфонов, создании одежды или строительстве жилищ.
Геометрия также способствует логическому мышлению и открытию закономерностей; это становится особенно актуально в нашем цифровом мире, насыщенном информацией.
Вот некоторые профессии, в которых знания геометрии будут крайне полезны: архитектор, программист, дизайнер, инженер, подрядчик, строитель, SMM-менеджер, декоратор, пилот, шофер, художник, астроном, спортсмен, музыкант и многие другие.
Изучение геометрии может показаться легким, поскольку мы ежедневно видим трехмерный мир и активно взаимодействуем с предметами, создаем чертежи, замеряем в уме. Все знания в геометрии базируются на научных концепциях, что позволяет нам лучше осознавать пространство.
Но почему изучение геометрии иногда вызывает трудности? Некоторые правила действительно необходимо запоминать.
Для глубокого понимания геометрии важно двигаться от простого к сложному. Многие теоремы могут казаться самоочевидными, однако эта очевидность зачастую перечеркивается в случае, когда рассматриваются различные рисунки. Не получится нарисовать все возможные ситуации, поскольку их число бесконечно. Поэтому крайне важно доказать предложенные теоремы, что позволяет уверенно в них ориентироваться.








